Multi-Layer Perceptrons (MLP) and Backpropagation algorithm

Single Layer Perceptron – This is the simplest feedforward neural network and does not contain any hidden layer. 

 Minsky and Papert mathematically analyzed Perceptron and demonstrated that single-layer networks are not capable of solving problems that are not linearly separable. As they did not believe in the possibility of constructing a training method for networks with more than one layer, they concluded that neural networks would always be susceptible to this limitation.

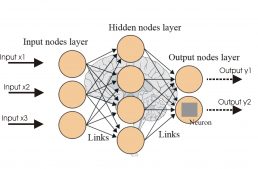
 The multilayer perceptron (MLP) is a neural network similar to perceptron, but with more than one layer of neurons in direct power. Such a network is composed of layers of neurons connected to each other by synapses with weights. Learning in this type of network is usually done through the back-propagation error algorithm, but there are other algorithms for this purpose, such as Rprop.


However, the development of the backpropagation training algorithm has shown that it is possible to efficiently train networks with intermediate layers, resulting in the most used artificial neural networks model currently, Perceptron Multi-Layer (MLP) networks, trained with the backpropagation algorithm.

 The backpropagation algorithm was originally introduced in the 1970s, but its importance wasn't fully appreciated until a famous 1986 paper byDavid Rumelhart, Geoffrey Hinton, and Ronald Williams. That paper describes several neural networks where backpropagation works far faster than earlier approaches to learning, making it possible to use neural nets to solve problems which had previously been insoluble. Today, the backpropagation algorithm is the workhorse of learning in neural networks.
Backpropagation is a method used in artificial neural networks to calculate a gradient that is needed in the calculation of the weights to be used in the network.[1] It is commonly used to train deep neural networks,[2] a term referring to neural networks with more than one hidden layer.[3]
Backpropagation is a special case of an older and more general technique called automatic differentiation. In the context of learning, backpropagation is commonly used by the gradient descent optimization algorithm to adjust the weight of neurons by calculating the gradient of the loss function. This technique is also sometimes called backward propagation of errors, because the error is calculated at the output and distributed back through the network layers.
The backpropagation algorithm has been repeatedly rediscovered and is equivalent to automatic differentiation in reverse accumulation mode. Backpropagation requires the derivative of the loss function with respect to the network output to be known, which typically (but not necessarily) means that a desired target value is known. For this reason it is considered to be a supervised learning method, although it is used in some unsupervised networks such as autoencoders. Backpropagation is also a generalization of the delta rule to multi-layered feedforward networks, made possible by using the chain rule to iteratively compute gradients for each layer. It is closely related to the Gauss–Newton algorithm, and is part of continuing research in neural backpropagation. Backpropagation can be used with any gradient-based optimizer, such as L-BFGS or truncated Newton.
Here an example of the code:

Comentários

Postar um comentário

Postagens mais visitadas deste blog

Akka vs. Spring Reactor personal comparison

Imagem
Akka vs. Spring Reactor personal comparison: I used for both a mass of Fake data of 200000 records for each. Both use the Reactive Streams Specification (Reactive Streams) Reactive Streams is an initiative to provide a standard for asynchronous flow processing with non-blocking return pressure. This includes efforts focused on runtime environments (JVM and JavaScript) as well as network protocols. What we want is asynchronous and non-blocking. A group of developers of companies like Netflix, Pivotal, RedHat, etc. met and converged to something called The Reactive Streams Specification.   Akka framework Akka is an Opensource framework. Akka is implemented from the agent model (originated in 1973 by Carl Hewitt), which provides a model for dealing with concurrent computing. Akka, the unit of execution is the Actor and his microservices are built as actors. An actor is lightweight and there may be several
Leia mais

Simple Application Microservices and MongoDB using Clean Architecture

Imagem
Simple Application Microservices and MongoDB using Clean Architecture Created in mid-2012 by Robert Cecil Martin ("Uncle Bob"), Clean Architecture has as main purposes to be independent of frameworks, easily testable, regardless of the user interface, that is, the user interface can change at will without this reflects in the rest of the system, be independent of database, since it maintains all business rules in the application itself and, finally, be independent of any external agent, and the business rules do not "see" the " outside world ". For start my application I studied some frameworks before choose some, at the end the choose was not for performance, just for an example I choose the fasted way to developed, easy understand, easy codification and quick production instead of best performance. You can ask me, why I would choose facility instead of performance ? First question, do you really need a truck
Leia mais

Adaline - Adaptive Linear Neuron

Imagem
Just continuing with my explanation about Artificial Neural Networks in a simple way. The Adaline  ( Adaptive Linear  Neuron or later  Adaptive Linear Element )  network, proposed by Widrow and Hoff in 1960, has the same structure as the Perceptron, differentiating only in the algorithm of training. She is an adaptive network, with the Inclusion of a pioneering algorithm for the training of  multi-layered networks, the training algorithm of the Delta rule, the Delta rule algorithm is based on the method of least squares, she has a smoother learning method. Their goal is Perform local iterations to get the function and thus set the values of the weights  when the minimum was found. Through an arbitrary point (vector of weights started randomly), the algorithm runs, at each iteration, the surface of the error function towards the point of Minimum. Adaline is a single layer neural network with multiple nodes where each node accepts multiple inputs and generates one output.
Leia mais