Adaline - Adaptive Linear Neuron

Just continuing with my explanation about Artificial Neural Networks in a simple way.

The Adaline (Adaptive Linear Neuron or later Adaptive Linear Element) network, proposed by Widrow and Hoff in 1960, has the same structure as the Perceptron, differentiating only in the algorithm of training.

She is an adaptive network, with the Inclusion of a pioneering algorithm for the training of multi-layered networks, the training algorithm of the Delta rule, the Delta rule algorithm is based on the method of least squares, she has a smoother learning method.

Their goal is Perform local iterations to get the function and thus set the values of the weights when the minimum was found.

Through an arbitrary point (vector of weights started randomly), the algorithm runs, at each iteration, the surface of the error function towards the point of Minimum.

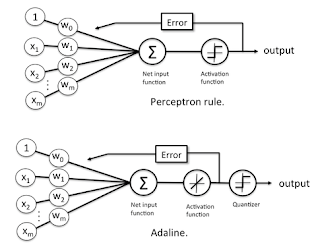
Adaline is a single layer neural network with multiple nodes where each node accepts multiple inputs and generates one output. Given the following variables:as

• ${\displaystyle x}$ is the input vector
• ${\displaystyle w}$ is the weight vector
• ${\displaystyle n}$ is the number of inputs
• ${\displaystyle \theta }$ some constant
• ${\displaystyle y}$ is the output of the model

then we find that the output is ${\displaystyle y=\sum _{j=1}^{n}x_{j}w_{j}+\theta }$. If we further assume that

• ${\displaystyle x_{0}=1}$
• ${\displaystyle w_{0}=\theta }$

then the output further reduces to: ${\displaystyle y=\sum _{j=0}^{n}x_{j}w_{j}}$

Learning algorithm

Let us assume:

• ${\displaystyle \eta }$ is the learning rate (some positive constant)
• ${\displaystyle y}$ is the output of the model
• ${\displaystyle o}$ is the target (desired) output

then the weights are updated as follows ${\displaystyle w\leftarrow w+\eta (o-y)x}$. The ADALINE converges to the least squares error which is ${\displaystyle E=(o-y)^{2}}$.^[6] This update rule is in fact the stochastic gradient descent update for linear regression.^[7]

Here an example of the both algorithms:

https://github.com/edsoncezar/neuralnetworks